• Best portfolio in the world!!! • • 🔥🔥🔥🔥🔥🔥🔥🔥🔥 •
EN FR

Project: Operations Research

Project Objective:

As part of the Operations Research course, this project has two parts: implementing and solving flow problems (computing the maximum flow and the minimum-cost flow for a given value), and then analyzing the complexity of the algorithms and measuring their performance (execution time and result consistency).

Visual Demonstration

Code Illustration
Code Illustration
Code Illustration

Algorithmic Structure

Start the program

    // Choose an action
    Choose between:
        1. Study an existing graph
        2. Create a random graph
                    
        If "Study an existing graph" is chosen
             Enter the graph number (e.g., 1, 2, 3...)
                If the graph has associated costs (number > 5)
                    Choose a method:
                        1. Compute maximum flow (Edmonds-Karp)
                        2. Compute maximum flow (Push-Relabel)
                        3. Compute minimum-cost flow
                            If "Minimum-cost flow" is chosen
                                Enter the desired flow value
                            Else
                                Choose a method:
                                  1. Compute maximum flow (Edmonds-Karp)
                                  2. Compute maximum flow (Push-Relabel)
                        View the results:
                            - Final matrix
                            - Flow
                            - Cost (if applicable)
                            - Execution time
                    
        If "Create a random graph" is chosen
            Choose between:
                1. Simple test
                2. Multiple tests (100 graphs)
                    Enter the graph size (number of vertices)
                    If "Multiple tests" is chosen
                        Enter the desired flow value
                        Choose a method:
                            1. Compute maximum flow (Edmonds-Karp)
                            2. Compute maximum flow (Push-Relabel)
                            3. Compute minimum-cost flow
                            If "Minimum-cost flow" is chosen
                                Enter the desired flow value
                        View the results:
                            - Final matrix
                            - Flow
                            - Cost (if applicable)
                            - Execution time
                        If multiple tests:
                            - Average execution time
                    
                    End the program

Detailed Explanation of the Project

Implemented algorithms and their complexities:

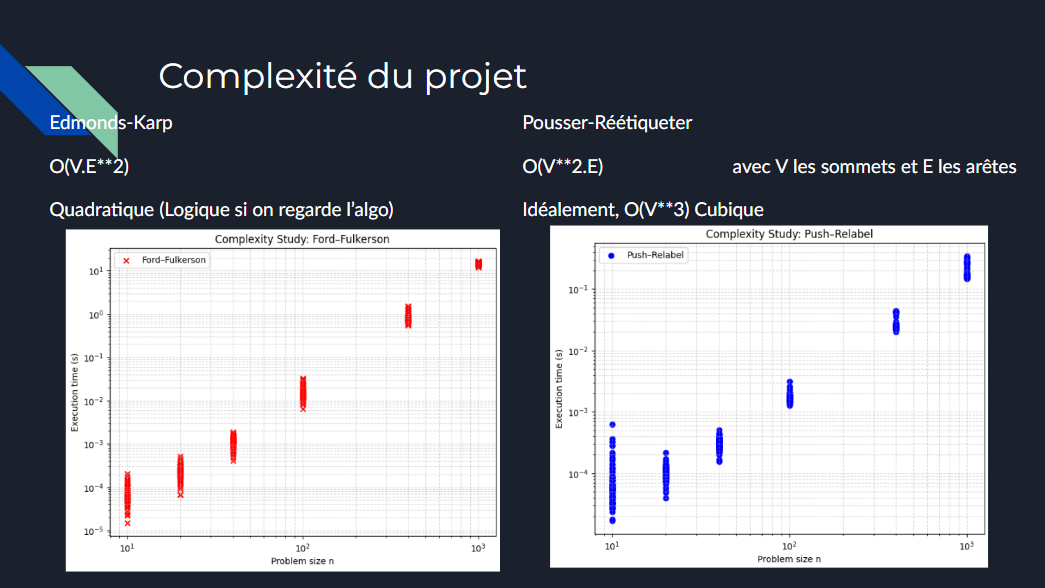
  • Edmonds-Karp (Ford-Fulkerson with breadth-first search): finds an augmenting path using BFS. Worst-case complexity is O(V·E²), where V is the number of vertices and E is the number of edges.
  • Push-Relabel: manages excess flow by locally adjusting vertex heights. Complexity is O(V²·E), often more efficient for dense graphs where E≫V.
  • Minimum-Cost Flow: uses Bellman-Ford to find the lowest cost path at each step. Typical complexity is O(F·E·V), where F is the desired flow value.