• Le meilleur portfolio au monde !!! • • 🔥🔥🔥🔥🔥🔥🔥🔥🔥 •
EN FR

Projet : Recherche Opérationnelle

Le but du projet :

Dans le cadre du cours de Recherche Opérationnelle, ce projet se décompose en deux volets : implémenter et résoudre des problèmes de flot (calcul du flot maximum et du flot de coût minimal pour une valeur donnée), puis analyser la complexité des algorithmes et mesurer leurs performances (temps d'exécution et cohérence des résultats).

Démonstration Visuelle

Illustration du code
Illustration du code
Illustration du code

Structure Algorithmique

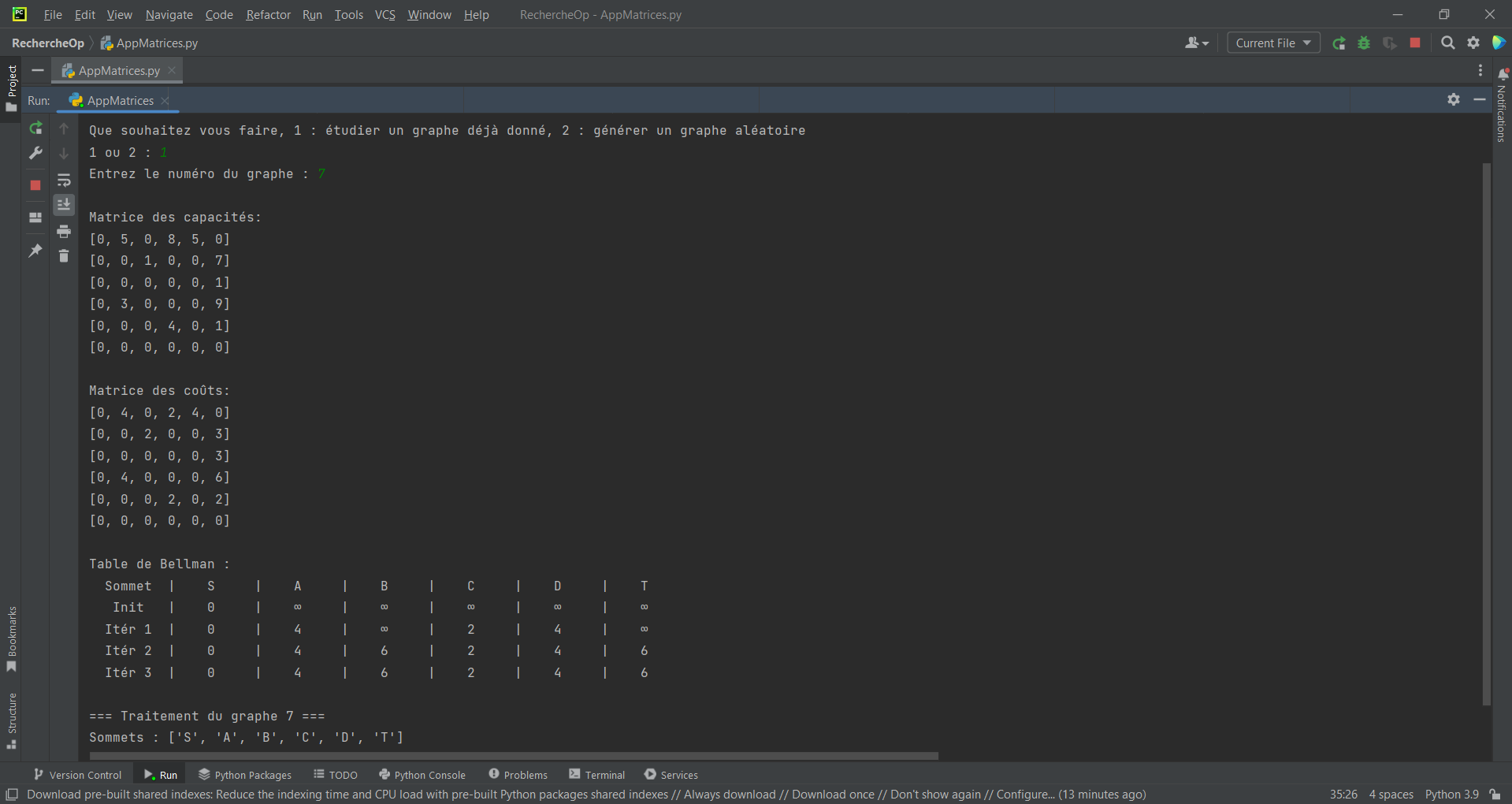
Démarrer le programme

    // Choisir une action
    Choisir entre :
        1. Étudier un graphe existant
        2. Créer un graphe aléatoire
                    
        Si choisir "Étudier un graphe existant"
             Entrer le numéro du graphe (par exemple, 1, 2, 3...)
                Si le graphe a des coûts associés (numéro > 5)
                    Choisir une méthode :
                        1. Calculer le flot maximal (Edmonds-Karp)
                        2. Calculer le flot maximal (Push-Relabel)
                        3. Calculer le flot à coût minimal
                            Si choisir "Flot à coût minimal"
                                Entrer la valeur de flot souhaitée
                            Sinon
                                Choisir une méthode :
                                  1. Calculer le flot maximal (Edmonds-Karp)
                                  2. Calculer le flot maximal (Push-Relabel)
                        Voir les résultats :
                            - Matrice finale
                            - Flot
                            - Coût (si applicable)
                            - Temps d'exécution
                    
        Si choisir "Créer un graphe aléatoire"
            Choisir entre :
                1. Test simple
                2. Test multiple (100 graphes)
                    Entrer la taille du graphe (nombre de sommets)
                    Si choisir "Test multiple"
                        Entrer la valeur de flot souhaitée
                        Choisir une méthode :
                            1. Calculer le flot maximal (Edmonds-Karp)
                            2. Calculer le flot maximal (Push-Relabel)
                            3. Calculer le flot à coût minimal
                            Si choisir "Flot à coût minimal"
                                Entrer la valeur de flot souhaitée
                        Voir les résultats :
                            - Matrice finale
                            - Flot
                            - Coût (si applicable)
                            - Temps d'exécution
                        Si test multiple, voir aussi :
                            - Temps moyen d'exécution
                    
                    Finir le programme

Explications Détaillées du projet

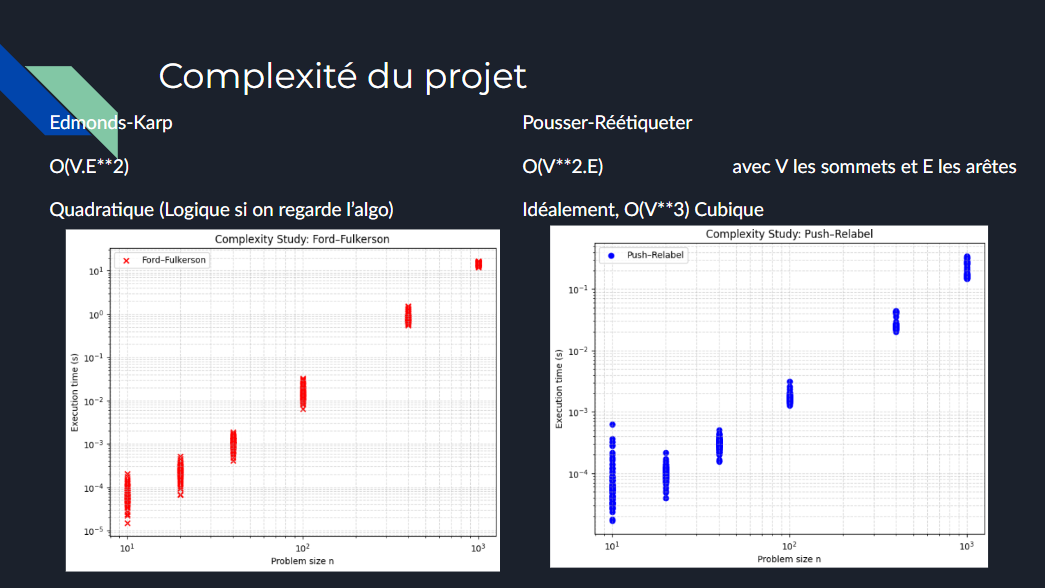
Algorithmes implémentés et complexités :

  • Edmonds-Karp (Ford-Fulkerson avec parcours en largeur) : cherche une chaîne améliorante par BFS. Complexité dans le pire des cas O(V·E²), avec V le nombre de sommets et E le nombre d'arêtes.
  • Push-Relabel : gère les excédents en ajustant localement la hauteur des sommets. Complexité O(V²·E), souvent plus efficace sur les graphes denses où E≫V.
  • Flot à coût minimal : utilise l'algorithme de Bellman-Ford pour obtenir à chaque étape le chemin de coût minimal. Complexité typique O(F·E·V), avec F la valeur du flot recherché.